최대 공약수를 구하는 방법
최대 공약수를 구하는 대표적인 알고리즘으로 "유클리드 호제법" 이 있습니다.
일반적으로는 최대 공약수를 구할 때 소인수분해를 이용해 공통된 소수들의 곱으로 표현할 수 있습니다.
하지만, 소인수분해는 코드로 구현하기 복잡하고 시간이 오래 걸릴 수 있다는 단점이 있습니다.
따라서, 우리는 유클리드 호제법을 사용해 더 간단하고 효율적인 방법으로 최대 공약수를 구하는 법을 배워보겠습니다.
이름의 유래 ✍️
"유클리드 호제법" 이라는 이름은 고대 그리스의 수학자 유클리드에서 유래했습니다.
이 알고리즘은 유클리드의 원론에 적혀있는 내용으로, 인류 최초의 알고리즘이라고 합니다.
"호제법"이라는 이름은 "번갈아 나누다" 라는 뜻에서 유래되었습니다.
즉, 큰 수를 작은 수로 나누고, 그 나머지를 다시 나누는 과정을 번갈아 반복하는 방식에서 비롯된 것입니다.

"간단한 이론이니 천천히 따라와 보게나"
유클리드 호제법 이해하기
유클리드 호제법을 이해하려면 먼저 MOD 연산을 알고 있어야 합니다.
MOD 연산이라는 단어가 조금 낯설게 느껴질 수 있지만, 사실 우리에게 익숙한 나머지 연산인 '%' 와 같은 개념입니다.
- ex) 10 MOD 4 = 2 ➡️ 10 % 4 = 2
유클리드 호제법을 이용하여 두 수 270과 192 의 최대 공약수(gcd)를 구하는 과정을 그림으로 살펴보겠습니다.

나머지가 0이 되는 순간의 작은 수 b를 최대 공약수로 선택한다.
"유클리드 호제법"을 활용하여 최소 공배수 구하기
최소 공배수 구하기 (백준1934)
- 최대 공약수를 알고 있다면 최소 공배수도 쉽게 구할 수 있습니다.
문제

출력

분류

코드
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
for (int i = 0; i < A; i++) {
st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
// 입력 받은 두 수 N과 M의 최대 공약수
int gcd = gcd(N, M);
// 최소 공배수 = N * M / 최대 공약수
System.out.println(N * M / gcd);
}
}
public static int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
}
풀이
최대 공약수 그림으로 이해하기
- 그림과 코드를 비교해보며 최대 공약수를 구해보도록 합시다.
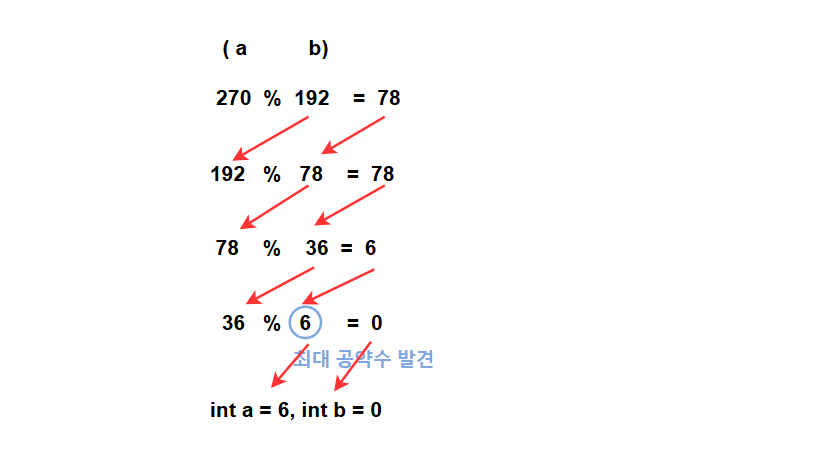
최대 공약수 코드로 이해하기
- 재귀함수를 통하여 최대 공약수를 구할 수 있습니다.
- b == 0 일 경우 최대 공약수 a 의 값을 return
public static int gcd(int a, int b) {
// b ==0 일 경우 최대 공약수 발견
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
최소 공배수 구하기
- 최소 공배수 공식: 두 수의 곱 N * M 을 최대 공약수로 나눈 값
// 입력 받은 두 수 N과 M의 최대 공약수
int gcd = gcd(N, M);
// 최소 공배수 = N * M / 최대 공약수
System.out.println(N * M / gcd);
정리 ✍️
오늘은 유클리드 호제법을 사용해 최대 공약수(gcd)를 효율적으로 구하는 방법을 배워보았습니다.
또한, 이를 활용한 문제를 통해 최소 공배수를 계산하는 방법도 함께 익혀보았죠.
이 이론은 한국 교육 과정에서 중학교 1학년 수학 교과서에서 짧게 소개되고 넘어가는 내용이라,
기억이 희미할 수도 있습니다. 하지만, 문제를 다시 접하고 이를 코드로 풀어보니 한층 더 흥미롭게 느껴지는거 같습니다 ☺️

"야, 너두 수학천재 할 수 있어."
'해피 코딩 > Algorithm' 카테고리의 다른 글
| [이론] 유니온 파인드 너무 쉬운데? (5) | 2024.12.24 |
|---|---|
| [백준 10986] '나머지 합' 가장 쉽게 이해하기 JAVA (1) | 2024.12.21 |
| [백준 1929] 문제로 이해하는 에라토스테니스의 체 JAVA (0) | 2024.12.16 |
| [이론] 병합 정렬 알고가기 (0) | 2024.12.12 |
| [이론] 버블 정렬 알고가기 (3) | 2024.12.05 |



