소수를 구하는 방법
소수를 구하는 대표적인 알고리즘으로 "에라토스테네스의 체" 가 있습니다.
이 알고리즘은 효율적으로 소수를 찾아내는 데 매우 유용하며,
대부분의 코딩테스트에서도 소수 판별 문제를 해결할 때 이 이론을 사용합니다.
오늘은 에라토스테네스의 체를 배워보며, 효율적인 소수 구하기의 원리를 이해해 봅시다! 😊
이름의 유래 ✍️
"에라토스테네스의 체" 라는 이름은 고대 그리스의 수학자인 에라토스테네스의 이름에서 유래했습니다.
그는 소수를 구하는 효율적인 방법을 체계적으로 처음 정리한 인물로 알려져 있습니다.
그리고 "체" 라는 이름은 우리가 곡식을 걸러내는 도구를 떠올리면 쉽게 이해할 수 있습니다.
즉, 소수가 아닌 수를 체로 걸러내듯 제거해 나가면, 마지막에 남는 숫자들이 바로 소수가 되는 것이죠.

"자네, 나와 함께 소수를 찾아보지 않겠나?"
에라토스테네스의 체 원리 이해하기
그림을 통해 1부터 30까지의 소수를 구하는 에라토스테네스의 체 원리를 쉽게 이해해 봅시다.
1️⃣ 1은 소수가 아니므로 2부터 시작합니다.

2️⃣ 선택한 수의 배수를 모두 삭제합니다. (현재의 경우 2의 배수를 모두 삭제)

3️⃣ 다음 지워지지 않은 수를 선택하고 선택한 수의 모든 배수를 삭제합니다.
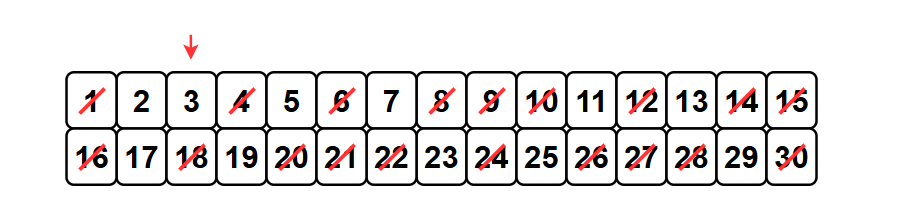
4️⃣ 앞의 과정을 배열의 끝까지 반복합니다.
5️⃣ 삭제되지 않은 수를 모두 출력합니다.
- 1부터 30까지의 소수 : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29

"에라토스테니스의 체" 를 사용하여 소수 구하기
소수 구하기(백준 1929)
문제

출력

분류

코드
public class Main {
static int[] A;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine()); // 1 30
int N = Integer.parseInt(st.nextToken()); // 1부터
int M = Integer.parseInt(st.nextToken()); // 30까지
// A 배열 초기화
A = new int[M + 1]; // 배열 크기[1~30]
for (int i = 2; i < M+1; i++) { // 1은 소수가 아니므로 2부터 시작
A[i] = i;
}
for (int i = 2; i <= Math.sqrt(M); i++) {
if (A[i] == 0){
continue;
}
for (int j = i * 2; j <= M ; j = j + i) { // i의 배수 제거
A[j] = 0;
}
}
for (int i = N; i <= M ; i++) {
if (A[i] != 0){ // 0이 아닌 수 즉, 제거 되지 않은 소수들 출력
System.out.println(A[i]);
}
}
}
}
풀이
제곱근 까지만 확인하는 이유
for (int i = 2; i <= Math.sqrt(M); i++)
만약 M이 30일 때,
`5 x 6 = 30`
sqrt(30)의 값은 약 5.47 이므로
- 모든 합성수는 두 수의 곱으로 이루어져 있기 때문
- sqrt(M)보다 큰 수는 이미 앞에서 다 지워진 상태라서 반복할 필요가 없음 ➡️ 반복 최소!
약수는 항사 짝을 이룬다는 특징을 활용하여 5까지만 확인하면 됩니다. 5보다 큰 숫자들은 이미 5 이하 숫자와 짝을 이루어 확인되었기 때문입니다.
정리 ✍️
오늘은 에라토스테네스의 체를 통해 효율적으로 소수를 구하는 방법을 배워보고, 이를 활용한 코드 구현까지 살펴보았습니다. ☺️
소수 판별 문제는 코딩테스트에서 자주 등장하는 유형 중 하나인 만큼, 이 알고리즘을 확실히 이해하고 직접 구현해보는 것이 중요합니다.
특히 제곱근까지만 확인하면 되는 이유와 배수 제거의 원리를 명확히 이해했다면, 소수 구하기 알고리즘을 한층 더 깊이 있게 다룰 수 있을 것입니다.
읽어주셔서 감사합니다 🙇

"어때, 쉽지?"
'해피 코딩 > Algorithm' 카테고리의 다른 글
| [백준 10986] '나머지 합' 가장 쉽게 이해하기 JAVA (1) | 2024.12.21 |
|---|---|
| [백준 1934] 문제로 이해하는 유클리드 호제법 JAVA (2) | 2024.12.16 |
| [이론] 병합 정렬 알고가기 (0) | 2024.12.12 |
| [이론] 버블 정렬 알고가기 (3) | 2024.12.05 |
| [백준 2018] 문제로 이해하는 투 포인터 JAVA (2) | 2024.12.05 |



