유니온 파인드
유니온 파인드(Union-Find)는 여러 노드가 있을 때, 특정 두 노드를 연결해 하나의 집합으로 묶는 union 연산과, 두 노드가 같은 집합에 속해 있는지를 확인하는 find 연산으로 구성된 알고리즘입니다.

근데 솔직히, 글로만 보면 알 듯 말 듯 애매하게 느껴지죠? 이건 마치 제 재능 같은 느낌이네요. 😅
그래서 한 마디로 정리하면 이렇게 이해하면 됩니다:
- union(a, b) 는 "a와 b를 합치라는 거구나! 둘을 같은 집합으로 묶어주는 거구나!"
- find(a) 는 "a가 속한 집합의 대표 노드를 찾아달라는 거구나!"

아직도 애매하다고 느껴지신다고요? 괜찮습니다!
이 글을 끝까지 읽으시면, 여러분도 유니온 파인드의 이론을 완벽하게 이해하실 수 있을 겁니다.
이 블로그를 발견한 당신, 이미 행운의 주인공입니다!! 😊
유니온 파인드 원리 이해하기
유니온 파인드를 더 쉽게 이해하기 위해 그림과 함께 설명해 보겠습니다. 시각적 자료를 통해 복잡한 개념도 간단하게 파악할 수 있을 겁니다.
1️⃣
처음에는 노드들이 서로 연결되어 있지 않기 때문에, 각 노드가 자기 자신의 대표 노드가 됩니다.
꿀팁💡 처음에는 모든 노드가 대표 노드이다.
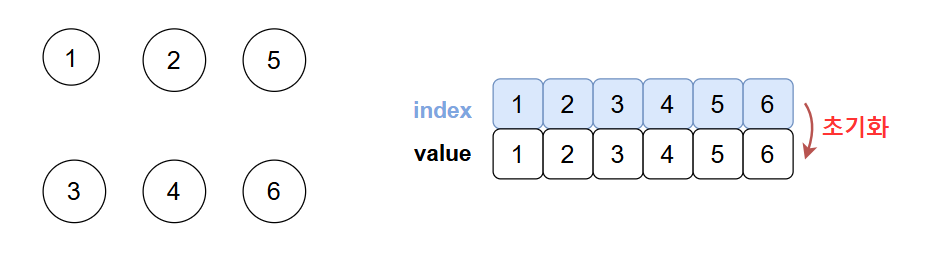
각 노드가 모두 대표노드 이므로 배열은 자신의 인덱스 값으로 초기화해 줍니다
2️⃣
이제 두 개의 노드를 선택하여 각각의 대표 노드를 찾아 연결하는 Union 연산을 수행합니다.
예시로, 다음과 같은 연산을 수행해 봅시다
- union(1, 4)
- union(5, 6)
- union(4, 6)
union(1,4)
대표 노드의 값을 자식 노드에 넣어줍니다 ➡️ 자식 노드 '4'의 값이 대표 노드 '1'로 변경됩니다.

union(5, 6)

3️⃣
'union(4, 6)'은 대표 노드가 아니므로 find연산을 이용하여 대표노드를 찾아 연결해 줍니다
- find(4) ➡️ 1
- find(6) ➡️ 5

따라서, find(6)의 대표 노드가 '5'이므로, 노드 '5'의 대표 노드를 '1'로 변경합니다.
은밀한 비법 전수 🕵️♂️
글을 읽으면서 구현 방법을 떠올리셨다면, 아마 "재귀 함수로 문제를 해결하면 되겠다!"는 생각이 드셨을 겁니다.
여기서 특별한 비법을 알려드리겠습니다!

✨ 은밀한 비법 - 경로 압축 ✨
대표 노드에 도달하면, 재귀 함수가 빠져나오는 과정에서 거치는 모든 노드의 값을 루트 노드 값으로 변경해 줍니다.
이 과정을 경로 압축이라고 하며, 이를 통해 트리의 깊이를 최소화할 수 있습니다.
경로 압축을 적용하면 이후의 find 연산이 훨씬 더 빠르게 처리되며, 알고리즘의 성능이 향상됩니다.
그림으로 차이점 비교하기
말로만 설명하면 이해하기 어려울 수 있으니, 그림으로 재귀 호출 전후의 차이를 비교해 보겠습니다.

이 배열을 활용해 경로 압축 적용 전후의 차이를 비교해 보겠습니다.
1️⃣ 경로 압축 적용 전
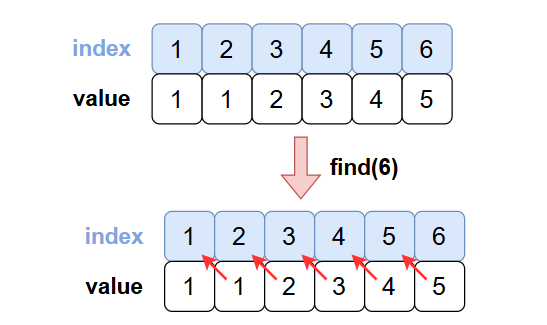
경로 압축이 적용되지 않은 상태에서는, 재귀 함수를 통해 find(6)의 대표 노드를 찾는 과정이 다음과 같이 진행됩니다.
- find(6) ➡️ 대표 노드 5를 찾음
- find(5) ➡️ 대표 노드 4를 찾음
- find(4) ➡️ 대표 노드 3을 찾음
- ...
- 최종적으로 대표 노드 1을 찾게 됩니다.
이 과정에서 트리의 깊이만큼 탐색해야 하므로, 트리가 깊어질수록 연산 시간이 증가하게 됩니다.
2️⃣ 경로 압축 적용 후
재귀 함수를 빠져나오면서 거치는 모든 노드의 값을 루트 노드 `1`의 값으로 변경하면, find(6)의 구조는 다음과 같이 변경됩니다.

이 과정이 완료되면, 트리의 깊이가 최소화되며, 그림에서처럼 find(6) 연산은 O(1)의 시간 복잡도를 갖게 됩니다.
트리 구조 비교하기 🌳
마지막으로, 트리 구조 그림을 통해 경로 압축 적용 전후의 차이를 비교해 보겠습니다.
그림을 보면 경로 압축이 트리의 깊이를 얼마나 효과적으로 줄이는지 한눈에 확인할 수 있습니다.
1️⃣ 경로 압축 적용 전
- 시간 복잡도⏱️: O(N)

2️⃣ 경로 압축 적용 후
- 시간 복잡도⏱️: O(1)

유니온 파인드 마무리 🚀
오늘은 유니온 파인드 알고리즘의 원리와 경로 압축을 활용한 최적화 방법에 대해 살펴보았습니다.
유니온 파인드는 간단한 아이디어에서 출발하지만, 효율성을 극대화하는 핵심 알고리즘 중 하나입니다.
다음 시간에는 문제를 풀며 유니온 파인드 알고리즘을 실제로 구현해 보겠습니다. 😊
'해피 코딩 > Algorithm' 카테고리의 다른 글
| [백준 10986] '나머지 합' 가장 쉽게 이해하기 JAVA (1) | 2024.12.21 |
|---|---|
| [백준 1934] 문제로 이해하는 유클리드 호제법 JAVA (2) | 2024.12.16 |
| [백준 1929] 문제로 이해하는 에라토스테니스의 체 JAVA (0) | 2024.12.16 |
| [이론] 병합 정렬 알고가기 (0) | 2024.12.12 |
| [이론] 버블 정렬 알고가기 (3) | 2024.12.05 |



